Game Development – Vectors
Basic Vector Math
Unless your game is only about clicking a few buttons or just text based adventure, you would at some level need to move things around in a 2d or 3d space. In order to know where our moving objects are going to be present in the next frame, we need to have some knowledge of Vector Math. Vectors contain information of direction andor magnitude. I would recommend reading about vector match in the Godot Documentation or watch videos on "Basic Vector Math" to understand the basics of Vector math, but just to give a quick overview, you can go through the following basics.
Note: I will be focusing only on Godot Game Engine but the concepts of Vectors are same in Unity, Unreal or any other game engine.
Basic Vector Math Overview
A vector can simply be understood as a piece of information, that contains information about a point or direction in 2D or 3D or 4D etc. space along with it’s magnitude. If we say a Vector (7, 9) it means that this vector is in the direction of 7 units on the x-axis and 9 units on the y-axis from the origin. A vector can be an absolute point in space relative to the origin or can be relative to another vector.
Mathematical representation
A vector in math is written as an alphabet with an arrow sign above it. For example, to write Vector A you write it as \vec{V}
If your vector is a unit vector (a vector whose magnitude is 1) you can use caret or hat sign above, like: \hat{V}
A vector can also be shown as matrix to show it’s elements:
\vec{V} = \begin{bmatrix}
V_x\\V_y\\V_z
\end{bmatrix} =
\begin{bmatrix}
2\\5\\9
\end{bmatrix} A point in space:
2D
Lets say horizontal axis is X and vertical axis is Y. A vector (3, 5) refers to a point where X is 3 and Y is 5.
3D
Same for X and Y but Z axis is forward and backward in space (in Godot and some other engines). A point (3, 5, 10) would mean where X is 3, Y is 5 and Z is 10.

In Godot, you can access the x, y using position or global_position in 2D
var my_position = positionor
var my_position = global_positionA point to not here is that in Godot 2D, the positive Y on the Y axis is downwards. The top left of the screen is (0, 0) and the bottom right is (screen_width, screen_height). In Godot 2D the units are in pixels.
For 3D on the other hand, you can use transform.
var my_position = transform.originor
var my_position = global_transform.originNOTE: the position or transform.origin will provide you with the position of the object relative to it’s parent node, while global_position or global_transform.origin will provide the position relative to the world origin.
Magnitude of a Vector
A magnitude of a vector is the distance between the origin and the vector coordinates. We can calculate the distance between two coordinates by calculating the magnitude of the direction of one from the other.

If we make a triangle out of a vector, we get a right angled triangle and we can use Pythagorean theorem to calculate the hypotenuse, which in the case of the Vectors is the magnitude of the vector. since we know the length of x and the length of y, the magnitude m is:
m^2 = {x^2 + y^2}
OR
m = \sqrt{x^2 + y^2}
For 3D:
m = \sqrt{x^2 + y^2 + z^2}
In Godot, you can use a Vector2 or Vector3 function length() to find the magnitude of the vector.
var target_pos := target.transform.origin
var dir_to_target := target_pos - transform.origin
var distance_to_target := dir_to_target.length()Adding/Subtracting Vectors
Adding vectors is very straight forward. You add the x, y and z of the first Vector to the x,y and z of the second vector respectively. Same for subtracting vectors, except instead of adding, you subtract the x, y and z respectively.
\vec{C} = \vec{A} + \vec{B}
\begin{bmatrix} C_x\\C_y\end{bmatrix} =
\begin{bmatrix} A_x\\A_y\end{bmatrix} +
\begin{bmatrix} B_x\\B_y\end{bmatrix} =
\begin{bmatrix} A_x + B_x\\A_y + B_y\end{bmatrix}Similarly,
\vec{C} = \vec{A} - \vec{B}
\begin{bmatrix} C_x\\C_y\end{bmatrix} =
\begin{bmatrix} A_x\\A_y\end{bmatrix} -
\begin{bmatrix} B_x\\B_y\end{bmatrix} =
\begin{bmatrix} A_x - B_x\\A_y - B_y\end{bmatrix}So for a vector A and B where
\vec{A} =
\begin{bmatrix} 2\\5 \end{bmatrix}and
\vec{B} =
\begin{bmatrix} 4\\2 \end{bmatrix}then
\vec{A} + \vec{B} =
\begin{bmatrix} 2 + 4\\5 + 2 \end{bmatrix} =
\begin{bmatrix} 6\\7 \end{bmatrix}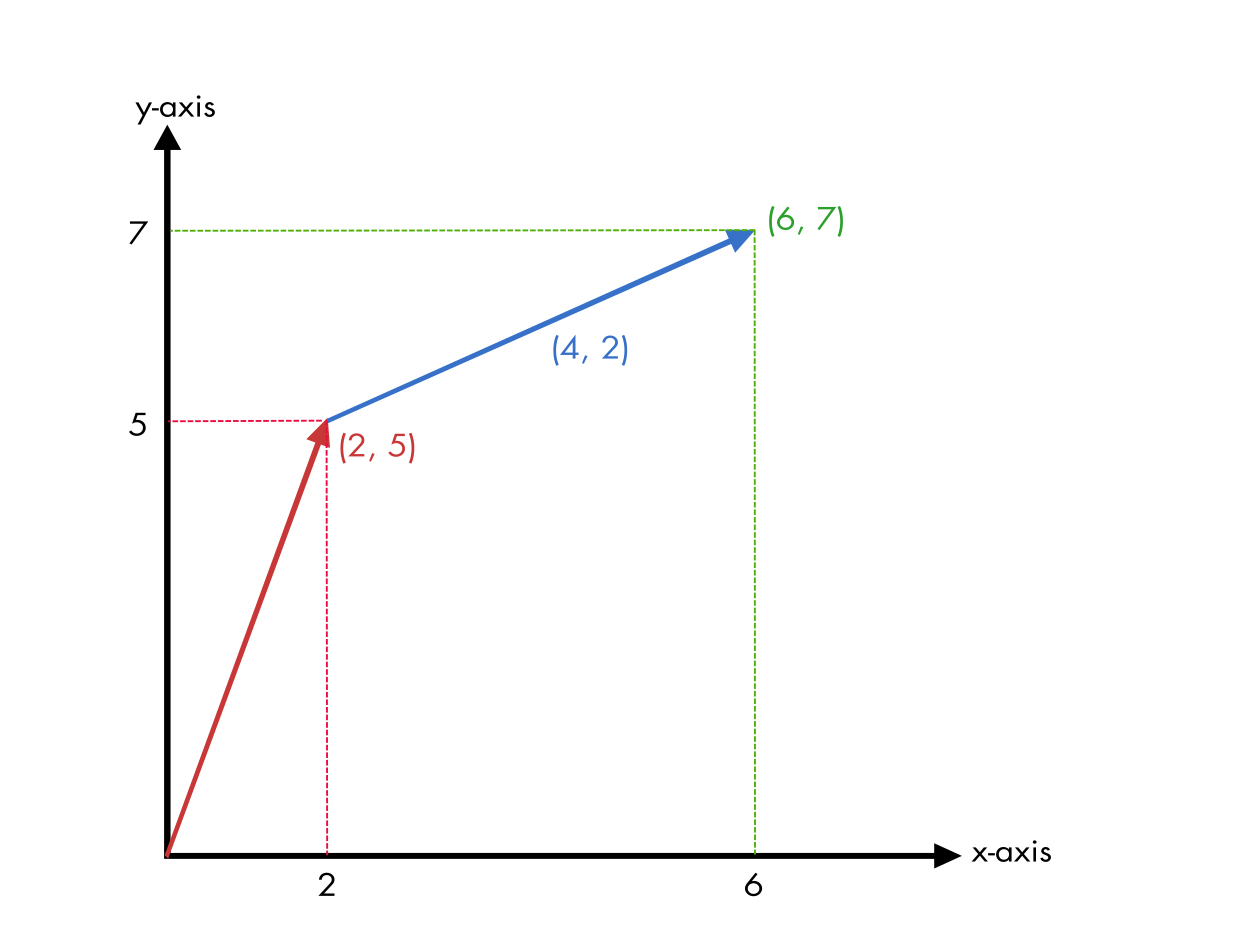
In the above diagram, you can also notice that the direction of the vector(6,7) from the vector(2, 5) is 4 units on x-axis and 2 units on the y axis. So, to calculate direction from one vector to the other you can use the formula: direction = vector2 – vector1:
\vec{D} = \vec{V_2} - \vec{V_1}
In Godot, you can just add subtract Vectors like you would any other variable or numbers. Make sur that the dimensions of the Vector are same.
var location_1 := Vector2(10, 29)
var location_2 := Vector2(37, 28)
var addition_v = location_1 + location_2
var subtraction_v = location_2 - location_1Normalized Vector
To get a normalized vector you can divide the x, y coordinates by it’s magnitude. This is used to make any Vector into a Unit Vector. Unit vectors are very useful in game development since they do not lose their direction information but don’t carry any magnitude information. Multiplying a unit vector to a scalar number makes the resulting vector’s magnitude same as the scalar number but, in the same direction as the unit vector.
You will need to normalize vectors when you are moving an object across multiple axes, but don’t need to modify the speed of the object moving.
Imagine you are moving a player in y axis at 5 units a frame. Your velocity would be (0,5). The magnitude of this vector is 5.
m = \sqrt{0^2 + 5^2} = 5
Now, Imagine the player presses the right key and you start moving the player 5 units in the x axis as well at the same time, adding (5,0) to the existing (0,5) velocity. the resulting velocity would be (5, 5). The magnitude of the final vector with both x and y is:
\sqrt{50} = 7.07(approx.)
You notice that the magnitude of the combined x and y axis is higher than when moving only in one direction. In a game, this would mean that the player would run faster when moving diagonally and slower when moving in only one direction. If your game, requires this behavior, then it is ok, but in most cases you DO NOT want this behavior. In real world, we do not walk or run faster when running diagonally than when we are moving just forward, sideways or backwards.
To solve this we can normalize the resulting vector and then multiply that unit vector to a scalar number of speed to move in any direction at constant speed. This is because the magnitude of a normalized vector is always 1. The direction of the normalized unit vector can be across multiple axes, but still the normalized vector’s magnitude is 1. So a movement of (5,5) when normalized will give us a
normalized (m) = (\frac{5}{\sqrt{50}})^2 + (\frac{5}{\sqrt{50}})^2
\rArr \frac{25}{50} + \frac{25}{50} = 1
so when we multiply 1 by any scalar number, the speed of movement will always be the scalar number.
In Godot, you can use the built in function normalized() to normalize Vector2 or Vector3.
var velocity : Vector2 = Vector2(12, 15)
# now normalize velocity
velocity = velocity.normalized()A direction:
In 2D:
If a vector is a direction, then (3, 5) would mean move 3 units to the right and 5 units up on the Y axis from the current position.
Getting Direction from 2 Vectors is also very simple. If A and B are two vectors in space, you can use the following formula to get the direction.
\vec{D} = \vec{B} - \vec{A}
\begin{bmatrix} D_x\\D_y\end{bmatrix} =
\begin{bmatrix} B_x\\B_y\end{bmatrix} -
\begin{bmatrix} A_x\\A_y\end{bmatrix}
In godot, you can just get the direction by subtracting the first Vector from the second Vector
# get the target object
export(NodePath) onready var target = get_node(target)
# get direction to target object
onready var dir = target.transform.origin - transform.origin
# normalize direction
dir = dir.normalized()
A dot product
a dot product between two vectors is a simple multiplication of 2 vectors V1 and V2 using the formula:
DP = \vec{V_1}.x * \vec{V_2}.x + \vec{V_1}.y * \vec{V_2}.y

In Game development, a dot product between two unit vectors can be very useful. A unit vector is a vector that has been normalized. To normalize a vector you divide it’s components by the magnitude.
For example, in our 3D game we might need to find out if the enemy is facing the player or not. The enemy needs to attack only when it is facing you, meaning the angle between the enemy’s facing direction and the player should ideally be less than 90 degrees.
So we can first get the direction towards the player with
var dir : Vector2 = player.global_position - global_positionor for 2D
var dir : Vector3 = player.global_position - transform.global_positionNow, we can normalize it using Godot’s helper function
dir = dir.normalized()Then, get the 2D plane on x and z because we want to ignore up and down look, just left and right
var dir_2d : Vector2 = Vector2(dir.x, dir.y)We do the same for enemies look direction, enemy facing -z
var enemy_dir_2d = Vector2(transform.basis.z.x, transform.basis.z.z)
var enemy_dir_2d = enemy_dir_2d.normalized()Now we can calculate the dot product between the two
var gap_angle = dir_2d.dot(enemy_dir_2d)
if gap_angle > 0:
print("enemy is facing the player")Vectors are not that hard to understand, but can be tricky if you are not used to them. It is very important to understand how the computers and game engines use them so that we can have full control of what is happening in the game. I will be writing more about Vectors in the subsequent tutorials, where we will talk about calculating normals using cross products and other situations like building meshes etc.
Please let me know your thoughts in the comments section or any topics you would like to learn about.
Thanks for Reading!
~ Vini
Feature Image by : Dan-Cristian Pădureț on Unsplash